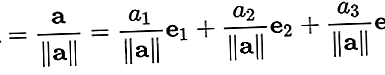Vektoren in Mathematik und Physik können als geometrische Objekte definiert werden, die Größe und Richtung haben. Der Vektor wird mit einem Pfeil dargestellt, wobei die Basis des Pfeils einen Fangpunkt (Startpunkt) eines Vektors zeigt. Die Länge des Pfeils gibt die Größe oder den Wert des Vektors an (je länger der Pfeil, desto größer der Wert oder Wert des Vektors und umgekehrt), während der Pfeil die Richtung des Vektors angibt.

Wenn der Vektor schriftlich am Punkt A beginnt und am Punkt B endet, kann er in einem kleinen Buchstaben geschrieben werden, über dem sich eine Linie / ein Pfeil befindet 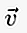 oder
oder 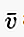 oder auch:
oder auch:
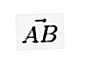
Arten von Vektoren
Der Vektor in der Mathematik ist in 4 Typen unterteilt, darunter:
Positionsvektor
Ein Vektor, dessen Startpunkt bei 0 (0,0) liegt und dessen Ende A (a1, a2) ist.
Null Vektor
"Vektor Null" (Nullvektor oderNullvektor) ist ein Vektor, dessen Länge "Null" ist. Die Schrift in dieser Vektorkoordinate ist (0,0,0) und wird normalerweise mit einem Symbol versehen  , oder0. Dieser Vektor unterscheidet sich von anderen Vektoren darin, dass er nicht normalisiert werden kann (dh kein Einheitsvektor ist ein Vielfaches des Nullvektors). Die Anzahl der Vektoren ist bei jedem Vektor Nullein istein (das ist,0+ein=ein).
, oder0. Dieser Vektor unterscheidet sich von anderen Vektoren darin, dass er nicht normalisiert werden kann (dh kein Einheitsvektor ist ein Vielfaches des Nullvektors). Die Anzahl der Vektoren ist bei jedem Vektor Nullein istein (das ist,0+ein=ein).
Der Nullvektor hat keine klare Vektorrichtung.
Einheitsvektor
ist ein Vektor mit der Länge "eins". Normalerweise wird der Einheitsvektor nur zur Richtungsangabe verwendet. Ein Vektor beliebiger Länge kann durch die Länge geteilt werden, um den Einheitsvektor zu erhalten. Dies ist als "Normalisieren" eines Vektors bekannt. Ein Einheitsvektor wird häufig durch eine "Kappe" über dem Kleinbuchstaben "a" wie in angezeigtein.
Einen Vektor normalisierenein = [ein1, ein2, ein3], dividiere den Vektor durch die Länge ||ein||. So:
Basisvektor
Ein Einheitsvektor, der senkrecht zueinander steht. In einem zweidimensionalen Raumvektor (R.2) hat nämlich zwei Basisvektoren 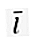 = (1, 0) und
= (1, 0) und 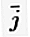 = (0, 1).
= (0, 1).
Ähnlichkeit zweier Vektoren
Zwei Vektoren gelten als gleich, wenn sie die gleiche Länge und Richtung haben

Eine Ausrichtung von zwei Vektoren
Zwei Vektoren werden als parallel (parallel) bezeichnet, wenn die Linie, die die beiden Vektoren darstellt, parallel ist.
Vektoroperationen
Skalarmultiplikation
Ein Vektor kann mit einem Skalar multipliziert werden, was ebenfalls zu einem Vektor führt. Der resultierende Vektor ist:
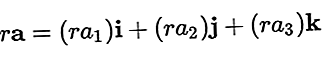
Vektoraddition und Vektorsubtraktion
Als Beispiel eines Vektors ein=ein1ich + ein2j + ein3k undb=b1ich + b2j + b3k
Das Ergebnis von a plus b ist: 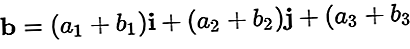
Die Vektorreduktion gilt auch durch Ersetzen des + -Zeichens durch ein - -Zeichen